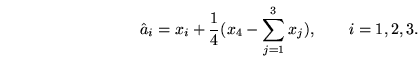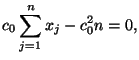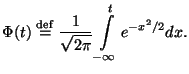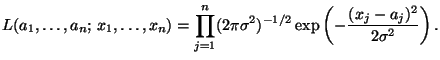Подпункты этого параграфа:
Начнем с очень простого примера. Предположим, что есть три образца некоторого
материала, массы которых 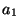 , , 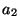 и и  неизвестны.
В наличии имеются весы, допускающие случайную нормально распределенную погрешность.
Образцы взвешивают раздельно, получая при этом показания весов неизвестны.
В наличии имеются весы, допускающие случайную нормально распределенную погрешность.
Образцы взвешивают раздельно, получая при этом показания весов 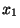 , ,
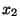 и и 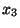 соответственно. Затем три образца взвешивают вместе
и получают показания весов соответственно. Затем три образца взвешивают вместе
и получают показания весов 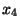 . Если допустить, что весы всякий раз
делают независимую ошибку, то, как правило, окажется, что . Если допустить, что весы всякий раз
делают независимую ошибку, то, как правило, окажется, что
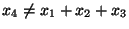 . .
Если бы мы допустили ``идеальную'' ситуацию, когда весы определяют массу
абсолютно точно, то, очевидно, в четвертом взвешивании не было бы никакого смысла.
Что касается реального опыта, когда к теоретическим массам добавляются случайные
ошибки, то интуитивно кажется, что четвертое взвешивание может содержать в себе
полезную информацию. Вопрос только в том, как ее правильно обработать.
Теперь сформулируем и обсудим общую модель, а затем вернемся к примеру.
Предположим, что неизвестные величины
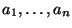 последовательно
измеряются некоторым измерительным прибором, прибавляющим случайную ошибку,
распределенную по нормальному закону последовательно
измеряются некоторым измерительным прибором, прибавляющим случайную ошибку,
распределенную по нормальному закону
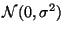 . Считая эти
измерения независимыми между собой и обозначая результаты этих измерений через . Считая эти
измерения независимыми между собой и обозначая результаты этих измерений через
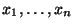 соответственно, запишем соответственно, запишем
где
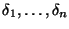 -- независимые случайные величины, распределенные
по закону -- независимые случайные величины, распределенные
по закону
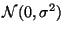 . Основное априорное допущение состоит
в том, что вектор . Основное априорное допущение состоит
в том, что вектор
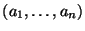 принадлежит некоторому линейному подпространству принадлежит некоторому линейному подпространству
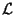 евклидова евклидова 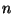 -мерного пространства -мерного пространства
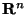 . Заметим,
что измерения . Заметим,
что измерения
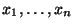 , полученные в результате опыта вовсе
не обязаны принадлежать , полученные в результате опыта вовсе
не обязаны принадлежать
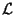 . Цель -- получить оценку для вектора
неизвестных параметров . Цель -- получить оценку для вектора
неизвестных параметров
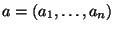 , используя данные измерений , используя данные измерений
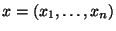 . .
Так как
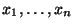 независимы и независимы и 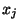 имеет распределение имеет распределение
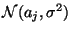 , нетрудно выписать функцию правдоподобия (т.е. совместную
плотность распределения , нетрудно выписать функцию правдоподобия (т.е. совместную
плотность распределения
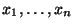 , см. также , см. также
 6.6): 6.6):
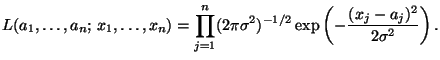 |
(38) |
Как и в
 6.6, в качестве искомой оценки будем искать точку 6.6, в качестве искомой оценки будем искать точку
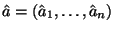 ,
в которой функция правдоподобия принимает максимальное значение:
Выражение (38) переписывается в следующем виде:
где ,
в которой функция правдоподобия принимает максимальное значение:
Выражение (38) переписывается в следующем виде:
где
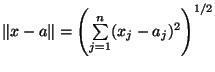 -- обычное евклидово расстояние между векторами в
-- обычное евклидово расстояние между векторами в
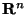 . Отсюда
видно, что максимальное значение достигается в такой точке . Отсюда
видно, что максимальное значение достигается в такой точке 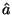 ,
для которой
Из курса линейной алгебры известно, что такая точка единствена и представляет
собой проекцию ,
для которой
Из курса линейной алгебры известно, что такая точка единствена и представляет
собой проекцию 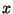 на подпространство на подпространство
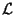 : :
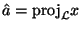 .
Поскольку задача свелась к минимизации суммы квадратов, этот метод получил название
метода наименьших квадратов. .
Поскольку задача свелась к минимизации суммы квадратов, этот метод получил название
метода наименьших квадратов.
Вернемся к нашему примеру и покажем, что четвертое взвешивание вовсе не было
напрасным. Попробуем извлечь из него полезную информацию. Построим линейную
модель, соответствующую этому опыту. Обозначим через 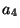 истинный суммарный
вес трех образцов. Теперь можем записать истинный суммарный
вес трех образцов. Теперь можем записать
Согласно сказанному выше, для того чтобы найти оценку неизвестных параметров
следует минимизировать по
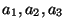 функцию
Оказывается, что минимум достигается в точке функцию
Оказывается, что минимум достигается в точке
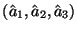 ,
где ,
где
Упражнение 7.1
Сравнить
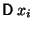 и и
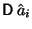 в предыдущем примере. Вспомнить
содержание в предыдущем примере. Вспомнить
содержание
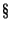 6.5 и сделать вывод. 6.5 и сделать вывод.
Пример 7.1
Независимая выборка из нормального распределения (Примеры 6.1 и 6.3)
можно считать частным случаем линейной модели (37), если выбрать
следующее подпространство
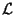 : :
Так как это подпространство одномерно, то
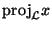 имеет
вид
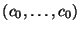 для некоторого 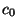 , которое может
быть найдено из условия ортогональности:
Приравнивая к нулю скалярное произведение этих векторов, получим
откуда
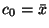 , следовательно,
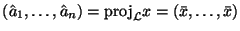 .
Этот результат полезно сравнить с оценкой математического ожидания, полученной
в Примере 6.10.
Замечание 7.1
Мы не коснулись здесь вопроса о том, как оценить дисперсию
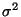 погрешности прибора в модели (37) в том случае, когда она является
неизвестной. Подробное обсуждение этого вопроса можно найти в книге [12, Гл. 3, § 3]
погрешности прибора в модели (37) в том случае, когда она является
неизвестной. Подробное обсуждение этого вопроса можно найти в книге [12, Гл. 3, § 3]
|  |

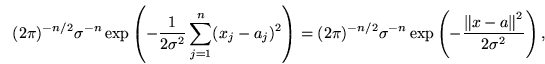
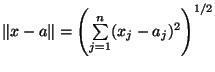 -- обычное евклидово расстояние между векторами в
-- обычное евклидово расстояние между векторами в