|
В настоящем параграфе под данными мы будем понимать набор из 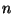 пар чисел: пар чисел:
 |
(40) |
причем пара
 представляет собой исход единичного наблюдения.
Роль чисел представляет собой исход единичного наблюдения.
Роль чисел  и и  в паре является различной и состоит
в следующем. Предполагается, что экспериментатор может абсолютно точно задавать
во время опыта значения в паре является различной и состоит
в следующем. Предполагается, что экспериментатор может абсолютно точно задавать
во время опыта значения  и затем измерять, допуская при этом случайную
ошибку, значение и затем измерять, допуская при этом случайную
ошибку, значение  . Например, . Например,  -- температура, выбираемая
в процессе эксперимента над образцом материала, -- температура, выбираемая
в процессе эксперимента над образцом материала,  -- длина образца
при соответствующей температуре. Число -- длина образца
при соответствующей температуре. Число  принято называть фактором,
а число принято называть фактором,
а число  -- откликом. Экспериментатор предполагает, что
между величинами -- откликом. Экспериментатор предполагает, что
между величинами  и и  существует функциональная зависимость вида
где существует функциональная зависимость вида
где  известные функции, а известные функции, а
 -- неизвестные
параметры. Предполагая, что ошибки, связанные с измерением отклика, независимы
и имеют распределение -- неизвестные
параметры. Предполагая, что ошибки, связанные с измерением отклика, независимы
и имеют распределение
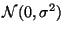 , получим следующую модель , получим следующую модель
Она называется регрессионной моделью. Задача
состоит в том, чтобы оценить неизвестные величины
 по данным наблюдений (40).
по данным наблюдений (40).
Для решения этой задачи эффективным оказывается подход, применяемый в предыдущих
параграфах: хорошей оценкой неизвестных параметров является та, которая ``минимизирует
сумму квадратов'':
Много дополнительных сведений о свойствах оценок наименьших квадратов в модели
регрессионного анализа, о проверке предпосылок к применению этой модели, а также
о проверке ее адекватности, можно почерпнуть из книги [13].
Иногда в качестве  берут степенные функции: берут степенные функции:
Таким образом, речь идет о том, чтобы приблизить неизвестную функциональную
зависимость  от от  полиномом вида полиномом вида
 . В этом случае говорят о задаче сглаживания наблюдений
. В этом случае говорят о задаче сглаживания наблюдений
 при помощи полинома. Более подробно об этой важной задаче,
в том числе о проблеме выбора степени полинома, можно прочитать в книге [12]. при помощи полинома. Более подробно об этой важной задаче,
в том числе о проблеме выбора степени полинома, можно прочитать в книге [12].
|  |