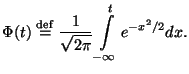Подпункты этого параграфа:
Здесь мы кратко обсудим распределение хи-квадрат и
распределение Стьюдента, играющие исключительную роль в статистике. Наше изложение
близко содержанию
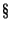 2.6 книги [13]. 2.6 книги [13].
Пусть
 -- независимые стандартные нормальные случайные
величины
( -- независимые стандартные нормальные случайные
величины
( ). ).  -распределением
с -распределением
с 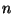 степенями свободы называется распределение следующей случайной величины: степенями свободы называется распределение следующей случайной величины:
 |
(44) |
Это распределение сосредоточенно на положительной полуоси и имеет плотность
где
 -- гамма-функция.
-- гамма-функция.
Упражнение 8.2
Начертить графики плотности
 при при  и и  . .
Упражнение 8.3
Найти
 и и
 . .
Квантили распределения
 будем обозначать будем обозначать
 , ,
 . По определению они являются решениями уравнения . По определению они являются решениями уравнения
 |
(45) |
где
 -- функция хи-квадрат распределения с
-- функция хи-квадрат распределения с 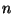 степенями свободы. На этом чертеже
изображены плотность степенями свободы. На этом чертеже
изображены плотность
 и ее квантиль. и ее квантиль.
Для значений функции распределения
 имеются таблицы,
из которых находят квантили. Кроме этого, хи-квадрат распределение интегрировано
в большое число прикладных компьютерных программ [13]. На странице имеются таблицы,
из которых находят квантили. Кроме этого, хи-квадрат распределение интегрировано
в большое число прикладных компьютерных программ [13]. На странице ![[*]](crossref.png) настоящей брошюры также приведена небольшая таблица квантилей хи-квадрат распределения.
настоящей брошюры также приведена небольшая таблица квантилей хи-квадрат распределения.
Это распределение получило свое название от псевдонима Student, которым
английский ученый Госсет подписывал свои работы по статистике.
Пусть
 -- независимые стандартные нормальные
случайные величины. Распределением Стьюдента
с -- независимые стандартные нормальные
случайные величины. Распределением Стьюдента
с 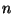 степенями свободы называется распределение следующей случайной величины: степенями свободы называется распределение следующей случайной величины:
 |
(46) |
Если вспомнить введенную формулой (44) случайную величину
 ,
то можно сказать, что отношение ,
то можно сказать, что отношение
 имеет распределение Стьюдента. Плотность этого распределения представляет собой
симметричную функцию, задаваемую формулой
По форме график функции
имеет распределение Стьюдента. Плотность этого распределения представляет собой
симметричную функцию, задаваемую формулой
По форме график функции
 напоминает график плотности стандартного
нормального закона, но с более медленным убыванием ``хвостов''. При напоминает график плотности стандартного
нормального закона, но с более медленным убыванием ``хвостов''. При
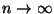 последовательность функций
последовательность функций
 сходится к функции сходится к функции
 ,
которая есть плотность распределения ,
которая есть плотность распределения
 . Чтобы понять, почему
этот факт имеет место, следует обратить внимание на то, что по закону больших
чисел знаменатель выражения (46) при . Чтобы понять, почему
этот факт имеет место, следует обратить внимание на то, что по закону больших
чисел знаменатель выражения (46) при
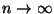 стремится к
стремится к
 . .
На чертеже представлены плотность распределения Стьюдента  и плотность
стандартного нормального закона. и плотность
стандартного нормального закона.
В дальнейшем нам понадобятся квантили распределения  , которые мы
будем обозначать , которые мы
будем обозначать
 , ,
 , ,
Небольшую таблицу квантилей распределения Стьюдента можно найти на странице ![[*]](crossref.png) . .
| 

 -- гамма-функция.
-- гамма-функция.
 -- функция хи-квадрат распределения с
-- функция хи-квадрат распределения с 


![[*]](crossref.png) .
.