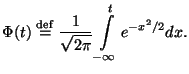|
 | ||||||||||||||||||||||||||||||||||||||||||||
2.3 Математическое ожидание
Так как случайная величина
Определение 2.3
Математическим ожиданием
случайной величины

Доказательство. Мы будем использовать следующий факт из курса математического анализа (см., например, [9, § 25, Теорема 1]). Пусть дан абсолютно сходящийся ряд. Тогда его члены можно произвольным образом переставлять и группировать, полученные в результате этого ряды будут сходиться к одному и тому же значению.
Пример 2.5
Пример 2.6
Пусть с.в.
Упражнение 2.1
Найти математическое ожидание пуассоновской случайной величины
| |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||