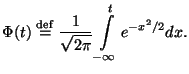|
В этом параграфе мы будем предполагать, что строго возрастающая функция
 есть функция распределения некоторой непрерывной случайной
величины есть функция распределения некоторой непрерывной случайной
величины  . В дальнейшем . В дальнейшем  -- число между -- число между  и
и  . .
Определение 3.9
Квантилью уровня  для
распределения , порождаемого функцией  , называется
число
 , являющееся решением уравнения
Другими словами,
 , где

-- функция, обратная к функции 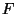 .
Из определения вытекает, что
 |
(18) |
где
 В частности, В частности,
 монотонно
растет по монотонно
растет по  . .
Замечание 3.6
Квантили часто называют также процентными точками распределения.
Доказательство.
Для определенности считаем, что  . Производя замену переменных
в интеграле и пользуясь четностью плотности, получим цепочку равенств . Производя замену переменных
в интеграле и пользуясь четностью плотности, получим цепочку равенств
Первая часть Предложения доказана, вторая вытекает из первой.

Если некоторая функция распределения  удовлетворяет тождеству удовлетворяет тождеству
 ,
то соответствующее ей распределение называется
симметричным. ,
то соответствующее ей распределение называется
симметричным.
|  |