|
 | ||||||||
3.5 Математическое ожидание и дисперсия абсолютно непрерывной случайной величины
Определение 3.8
Математическим ожиданием
случайной величины
По определению математическое ожидание существует тогда и только тогда, когда интеграл сходится абсолютно. Формула (17) аналогична формуле (7) для дискретных случайных величин.
Предложение 3.2 (Без доказательства.)
Пусть
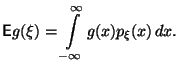
В частности,
Упражнение 3.8
Вычислить математическое ожидание и дисперсию равномерного
и показательного распределений (см. определения в
Упражнение 3.9
Доказать, что для случайной
величины
| |||||||||
| |||||||||
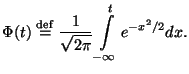
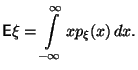
 Теперь понятно, как вычислять дисперсию
Теперь понятно, как вычислять дисперсию