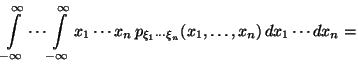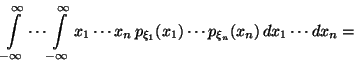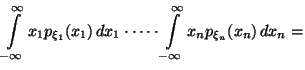|
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.3 Независимость случайных величин
Следующее определение обобщает понятие независимости, данное в
Следствие 4.3
Случайные величины
Упражнение 4.4
Доказать Следствие 4.3.
Предложение 4.3
Если
Доказательство. При доказательстве поочередно пользуемся Определениями 4.1, 4.3 и 3.5:
Замечание 4.1
Такое же утверждение имеет место для любого конечного числа
случайных величин
Предложение 4.4
Если
Доказательство. Доказательство просто -- последовательно применяем Предложение 4.2, Следствие 4.3 и определение (17):
Доказательство.
Достаточно показать, что
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||