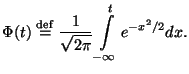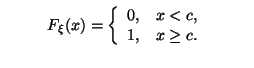Определение 3.5   Функцией распределения случайной величины называется функция , определяемая следующим образом

(16)

Предложение 3.1   Имеют место следующие общие свойства функций распределения:

1. .
2. -- неубывающая функция:
       если

3. Пределы на бесконечности
   
   
   

4. Функция непрерывна справа в каждой точке:
   

Упражнение 3.2  

Показать, что у функции распределения в каждой точке существует предел слева, т.е. существует

Упражнение 3.3   Показать, что множество точек разрыва функции не более, чем счетно. (Точка разрыва: .)

Пример 3.1   Простейший случай -- константа: . В этом случае

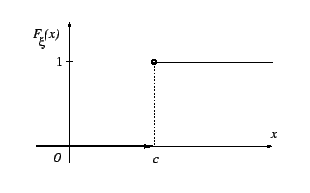
Пример 3.2  

Дискретная случайная величина -- число выпавших очков на игральной кости:

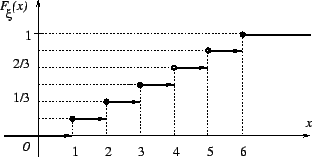
Пример 3.3  

Более общая дискретная случайная величина

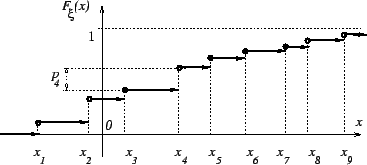
Замечание 3.4   Каков вероятностный смысл точки разрыва функции распределения ? Ответ на этот вопрос получится, если в (16) положить , а устремить к  слева:

(Чтобы строго обосновать этот вывод, следует воспользоваться свойствами вероятностной меры из   3.1.) Таким образом, функция распределения имеет разрыв в точке тогда и только тогда, когда . Более того, величина скачка в точке разрыва совпадает с этой вероятностью.