|
 | ||||||||
6.4 Выборочное среднее и выборочная дисперсияИногда исследователь ставит перед собой более конкретную проблему: как, основываясь на выборке, оценить интересующие его числовые характеристики неизвестного распределения, не прибегая к приближению этого распределения как такового, то есть без построения выборочных функций распределения, гистограмм и т.п.
В данном параграфе мы обсудим простые (но, как увидим в дальнейшем, весьма хорошие)
выборочные аппроксимации для математического ожидания и дисперсии. Замечательно
то, что они применимы в очень общей ситуации. Мы будем предполагать, что независимая
выборка
Определение 6.2
Величины, вычисляемые по выборке, и называются выборочным средним и выборочной дисперсией.
Следует особо подчеркнуть, что определенные выше величины зависят только от
выборки. Следующее предложение объясняет, почему естественно считать
Предложение 6.1
Математические ожидания Дисперсия
Доказательство. Используя линейность математического ожидания, получим 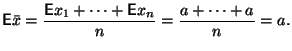
Так как выборка независимая, то
Покажем теперь, что
Это утверждение свидетельствует о том, что
Замечание 6.4
Для оценивания дисперсии по выборке может быть использована также функция 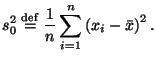
Доказательство.
Как и при доказательстве Предложения 6.1 без ограничения общности
будем считать, что
Применяя закон больших чисел в форме Хинчина к последовательности 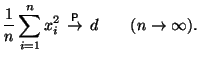
Замечание 6.5
Здесь мы воспроизводим замечание о вычислениях, приведенное в [12, с. 116].
Из соотношения (33) вытекает следующее представление для Математически формулы (30) и (34) дают одно и то же значение. Но, если нам необходимо вручную вычислить выборочную дисперсию, то следует это делать только по формуле (30), так как вычисления по формуле (34) потребовали бы учета намного большего числа значащих цифр, чем в случае применения формулы (30).
Имеется большое число практически важных приемов, призванных облегчить вычислительную работу с конкретными числовыми выборками. Для знакомства с ними рекомендуем читателю обратиться к книге [11]. В настоящее время существует много прикладных компьютерных программ, которые можно и нужно использовать для обработки числовых данных. С некоторыми наиболее популярными специализированными статистическими пакетами (Stadia, StatGraphics) можно познакомиться по книге [13], к которой также приводится их сравнение. Для статистической обработки небольших массивов данных вполне подойдет любой хороший универсальный математический пакет (Mathematica, Maple, Matlab).
Пример 6.5
Вычислим выборочное среднее и выборочную дисперсию для числовых данных Примера 6.4
на странице
| |||||||||
| |||||||||
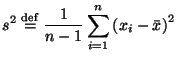
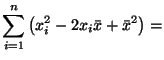
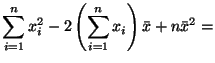
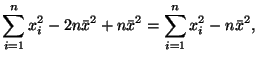
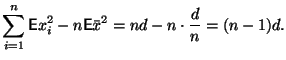
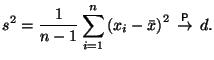
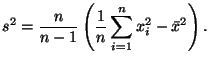
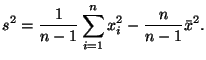
![[*]](crossref.png)