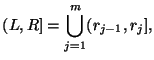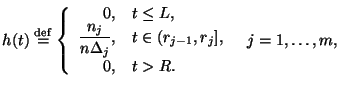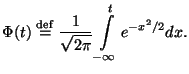|
Помимо эмпирических функций распределения, наглядное (но,
вместе с тем, довольно приближенное) представление о неизвестном распределении
можно получить при помощи гистограмм. Пусть
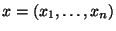 -- независимая выборка из неизвестного распределения
-- независимая выборка из неизвестного распределения 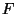 . Выберем два
числа . Выберем два
числа 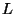 и и 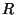 , ,
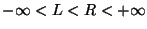 , такими, чтобы все числа , такими, чтобы все числа
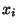 попали внутрь интервала попали внутрь интервала 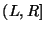 . Разобъем этот интервал на
конечное число меньших интервалов: . Разобъем этот интервал на
конечное число меньших интервалов:
где
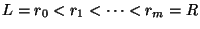 . Обозначим через . Обозначим через
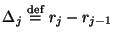 длины интервалов разбиений. Теперь произведем так называемую группировку
данных (выборки), а именно, для каждого интервала разбиения
длины интервалов разбиений. Теперь произведем так называемую группировку
данных (выборки), а именно, для каждого интервала разбиения
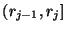 объединим в группу те
объединим в группу те 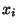 , которые попали в этот интервал. Пусть , которые попали в этот интервал. Пусть 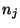 -- число таких элементов выборки:
Определим функцию
График функции
-- число таких элементов выборки:
Определим функцию
График функции 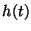 и называется гистограммой. и называется гистограммой.
Таким образом, гистограмма представляет собой график кусочно-постоянной
функции, такой, что площадь столбца с основанием, например,
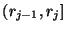 равна частоте попадания измерений в этот интервал группировки. Вспоминая материал
равна частоте попадания измерений в этот интервал группировки. Вспоминая материал
 3.4,
можно заключить, что гистограмма является выборочным аналогом плотности распределения. 3.4,
можно заключить, что гистограмма является выборочным аналогом плотности распределения.
При построении гистограмм мы имеем свободу в выборе интервала 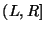 ,
числа интервалов разбиения ,
числа интервалов разбиения 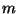 и самих точек и самих точек
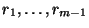 .
Для получения хороших приближений для плотности неизвестного распределения следует
всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по
выбору этих параметров таковы. .
Для получения хороших приближений для плотности неизвестного распределения следует
всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по
выбору этих параметров таковы.
- Значение
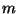 должно быть существенно меньше, чем объем выборки должно быть существенно меньше, чем объем выборки 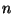 ,
но вместе с тем не слишком малым, чтобы гистограмма имела достаточно подробный
профиль. ,
но вместе с тем не слишком малым, чтобы гистограмма имела достаточно подробный
профиль.
- Интервалы разбиения следует выбирать так, чтобы каждый из них содержал ``достаточно
много'' элементов выборки. Если в группах недостаточно большое число данных,
то возможные случайные флуктуации их числа приводят к значительным искажениям
реальной картины.
При больших объемах выборки нередко берут разбиение интервала 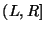 на
подинтервалы одинаковой длины. на
подинтервалы одинаковой длины.
|  |