|
 | |||||||||||||||||||||
3.4 Непрерывные случайные величиныПодпункты этого параграфа:
Легко видеть (см. Замечание 3.4), что случайная величина
непрерывна тогда и только тогда, когда
Важный класс непрерывных случайных величин -- абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.
Определение 3.7
Случайная величина

Функция
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.

Замечание 3.5
Если плотность
Следствие 3.2
Если
| ||||||||||||||||||||||
 |
 |
2) Показательное распределение
с параметром
![]()
![]()
 |
 |
Показательное распределение называют также экспоненциальным.
3) Нормальное (или
гауссовское) распределение
![]() ,
,
![]() ,
, ![]() :
:


Стандартное нормальное
распределение --
![]() :
:
|
|
 |
|
След.: 3.5 Математическое ожидание и ...
Пред.: 3.3 Функция распределения случайной ... Вверх: 3 Общие случайные величины ... |
Оглавление
Предметный указатель |
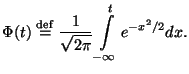
 ,
,


