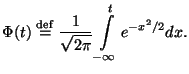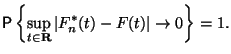 | |||||||||
 |
|
 | |||||||
 |
|||||||||
6.2 Эмпирическая функция распределения
В главе 3 шла речь о том, что все важнейшие характеристики
случайной величины могут быть выражены в терминах ее функции распределения.
В задачах математической статистики функция распределения (теоретическая) всегда
является неизвестной. Замечательно то, что основываясь на выборке, можно построить
хорошее приближение для неизвестной функции распределения
Пусть, как и прежде,
Определение 6.1
Эмпирической функцией распределения
 есть отношение числа элементов выборки, не превосходящих  ,
к объему выборки.
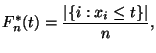
Замечание 6.1
Слово ``эмпирическая'' в Определении 6.1 означает, что функция вычисляется по данным опыта (эмпирическим данным), то есть, по выборке. По этой же причине для этого понятия иногда употребляют термин выборочная функция распределения.
Замечание 6.2
Легко видеть, что
Замечание 6.3
Как следует из Определения 6.1, значение функции
Оказывается, что в пределе
Этот факт имеет совершенно общий характер и называется теоремой Гливенко. Ее доказательство выходит за рамки данного курса. Желающие могут найти его в книге [4].
Упражнение 6.1
Доказать следующий ослабленный вариант утверждения (28): для любых
фиксированных
 ,
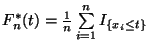и применить к последовательности независимых бернуллиевских случайных величин
 2.12).
| | ||||||||
А.Д. Манита, 2001-2011
| |||||||||
.
-- независимая выборка
из неизвестного распределения 
.
, вычисляемая
по выборке
различны, то в каждой точке 
. Если какие-либо из 
в точке 
.
В этом обозначении переменная 
-- фиксированные параметры. С другой стороны,
выборочная функция распределения
и
