Подпункты этого параграфа:
Всюду в этом параграфе мы рассматриваем независимые выборки
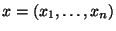 из нормального распределения
из нормального распределения
 . Мы построим доверительные
интервалы для параметров распределения при различных предположениях относительно
статистической модели. . Мы построим доверительные
интервалы для параметров распределения при различных предположениях относительно
статистической модели.
Предположим, что параметр  неизвестен, а дисперсия неизвестен, а дисперсия
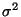 -- известное фиксированное число. Пусть
-- известное фиксированное число. Пусть 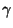 -- доверительная вероятность.
Применим метод, изложенный в -- доверительная вероятность.
Применим метод, изложенный в
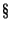 8.1. Выберем функцию 8.1. Выберем функцию
Из Упражнения 4.7 вытекает, что  имеет нормальное
распределение. Нетрудно видеть, что это стандартное нормальное распределение имеет нормальное
распределение. Нетрудно видеть, что это стандартное нормальное распределение
 . Следовательно, . Следовательно,
 . Выбирая . Выбирая
 и
и
 , ,
 ,
заключаем, что неравенство
выполнено с вероятностью ,
заключаем, что неравенство
выполнено с вероятностью 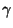 . Решая его, находим доверительный интервал:
Если теперь заметить, что . Решая его, находим доверительный интервал:
Если теперь заметить, что
 , то , то
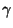 -доверительный интервал можно записать еще проще:
Замечательно то, что выборочное среднее является серединой этого интервала,
а его длина стремится к нулю с увеличением объема выборки. -доверительный интервал можно записать еще проще:
Замечательно то, что выборочное среднее является серединой этого интервала,
а его длина стремится к нулю с увеличением объема выборки.
Здесь среднее  считается известным фиксированным числом, а дисперсия считается известным фиксированным числом, а дисперсия
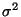 выступает в роли неизвестного параметра. Положим выступает в роли неизвестного параметра. Положим
Так как 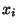 -- --
 , то , то
 имеет стандартное нормальное распределение. Тем самым, функция
имеет стандартное нормальное распределение. Тем самым, функция  имеет имеет
 -распределение с -распределение с 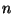 степенями свободы, никаким образом
не зависящее от неизвестного параметра степенями свободы, никаким образом
не зависящее от неизвестного параметра
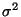 . Обозначая через . Обозначая через
 квантили этого распределения и фиксируя некоторые квантили этого распределения и фиксируя некоторые
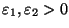 ,
такие, что ,
такие, что
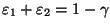 , приходим к неравенству , приходим к неравенству
 |
(47) |
которое выполнено с вероятностью 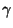 . Откуда получаем . Откуда получаем 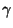 -доверительный
интервал для -доверительный
интервал для
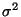 : :
Теперь оба параметра  и и
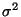 будем считать неизвестными.
Нас интересует доверительный интервал для будем считать неизвестными.
Нас интересует доверительный интервал для
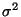 . В этом смысле
параметр . В этом смысле
параметр  является мешающим. Выберем является мешающим. Выберем
Заметим, что функция  определена таким образом, что при заданной выборке
ее значения зависят лишь от параметра определена таким образом, что при заданной выборке
ее значения зависят лишь от параметра
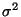 . Что касается распределения
случайной величины . Что касается распределения
случайной величины
 , то по теореме Фишера
(см. , то по теореме Фишера
(см.
 8.3) оно является 8.3) оно является  -распределением с -распределением с  степенями свободы и, следовательно, не зависит от неизвестных параметров. Фиксируя
степенями свободы и, следовательно, не зависит от неизвестных параметров. Фиксируя
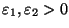 , такие, что , такие, что
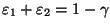 ,
и рассуждая как в (47), приходим к следующему ,
и рассуждая как в (47), приходим к следующему 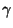 -доверительному
интервалу для -доверительному
интервалу для
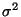 :
который, используя обозначение (30), можно переписать так :
который, используя обозначение (30), можно переписать так
Как и в предыдущем пункте, оба параметра  и и
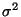 считаются
неизвестными, при этом считаются
неизвестными, при этом
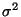 является мешающим параметром. По теореме Фишера является мешающим параметром. По теореме Фишера
 и 
независимы и имеют распределения
 и и  -распределение
с -распределение
с  степенью свободы соответственно. Следовательно, отношение степенью свободы соответственно. Следовательно, отношение
 |
(48) |
имеет распределение Стьюдента с  степенью свободы. Выберем функцию степенью свободы. Выберем функцию
 равной правой части (48):
где равной правой части (48):
где  -- выборочная дисперсия, определенная формулой (30).
Функция -- выборочная дисперсия, определенная формулой (30).
Функция  не зависит явно от мешающего параметра не зависит явно от мешающего параметра
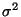 .
Обозначая через .
Обозначая через
 квантиль распределения Стьюдента
с квантиль распределения Стьюдента
с  степенью свободы, получим, что неравенство
выполнено с вероятностью степенью свободы, получим, что неравенство
выполнено с вероятностью 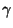 . Отсюда получаем . Отсюда получаем 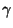 -доверительный
интервал для -доверительный
интервал для  :
Так как распределение Стьюдента симметрично, то по Предложению 3.3
Поэтому доверительный интервал можно записать в виде :
Так как распределение Стьюдента симметрично, то по Предложению 3.3
Поэтому доверительный интервал можно записать в виде
 |
(49) |
Таким образом, выборочное среднее  является серединой этого интервала. является серединой этого интервала.
Пример 8.2
Обратимся к Примеру 6.4. Предположим, что каждая из
выборок 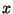 и и  взята из нормального распределения с неизвестными
параметрами -- взята из нормального распределения с неизвестными
параметрами --
 и и
 соответственно. (О том, на основании чего можно сделать такое допущение, мы
поговорим позже в
соответственно. (О том, на основании чего можно сделать такое допущение, мы
поговорим позже в
 9.5.) 9.5.)
Наша цель -- найти доверительные интервалы для  и и  ,
теоретических значений содержания углерода и прочности на разрыв стали GS50.
Напомним, что объем каждой из выборок ,
теоретических значений содержания углерода и прочности на разрыв стали GS50.
Напомним, что объем каждой из выборок  . Зафиксируем доверительную
вероятность, близкую к единице, скажем . Зафиксируем доверительную
вероятность, близкую к единице, скажем
 . По таблице распределения
Стьюдента на стр. . По таблице распределения
Стьюдента на стр. ![[*]](crossref.png) определим приближенно, что определим приближенно, что
 .
Вспоминая значения .
Вспоминая значения  и и  , найденные в Примере 6.5
на стр. , найденные в Примере 6.5
на стр. ![[*]](crossref.png) , вычисляем , вычисляем
и, пользуясь формулой ( 49), получаем  -доверительный
интервал для процентного содержания углерода
и  -доверительный интервал для значения прочности на разрыв
|  |






 и
и 


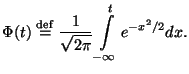


![[*]](crossref.png)