|
 | ||||||||
9.5 Проверка нормальности при помощи вероятностной бумаги
Этот простой графический метод часто используют для первоначальной прикидки,
правдоподобно ли предположение о том, что независимая выборка
Чтобы пояснить идею этого метода, сформулируем вспомогательное утверждение.
Пусть
Лемма 9.1
Рассмотрим отображение
Доказательство.
Достаточно заметить, что

Предположим, что в нашей выборке
Из Определения 6.1 легко вытекает, что в этом случае эмпирическая функция распределения может быть выражена формулой В частности,  . .
С другой стороны, теорема Гливенко утверждает, что при большом объеме выборки
эмпирическая функция распределения близка к теоретической функции распределения.
Принимая во внимание Лемму 9.1, заключаем, что если выборка
должны приблизительно оказаться на одной прямой линии (а именно, на прямой
Замечание 9.2
Мы намеренно не включаем в перечень (55) точку, соответствующую
Таким образом, мы пришли к очень простому глазомерному способу проверки нормальности выборки: наносим на плоскость точки 
Чтобы было удобнее наносить эти точки, прибегают к так называемой вероятностной
бумаге. Вероятностная бумага получается выбором неравномерной шкалы координат
вдоль оси ординат. А именно, на расстоянии
Замечание 9.3
В силу того, что данные наблюдений и измерений, как правило, округлены до некоторого
знака, предположение о том, что все
Замечание 9.4
Мы не используем точку
Пример 9.1
Вернемся к нашему числовому Примеру 6.4 и зададимся вопросом,
насколько в Примере 8.2 было обоснованным предположение о нормальности
выборок
Для выборки
Для выборки
Видно, что и в том, и в другом случае точки располагаются вблизи некоторой прямой
линии. Таким образом, имеются основания для гипотез о нормальности выборок
Большое число естественно-научных примеров, при анализе которых используется вероятностная бумага, содержится во второй части книги [12].
| |||||||||
| |||||||||
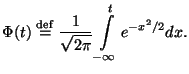
 .
.
![[*]](crossref.png)


