|
Здесь мы рассмотрим простейшие случайные величины, тесно связанные с событиями.
Они очень удобны при изучении произвольных случайных величин.
Определение 2.5
Индикатором события 
называется случайная величина
 :
Другими словами,  , если происходит событие , если происходит событие  , и , и  ,
если событие ,
если событие  не происходит. Таким образом, не происходит. Таким образом,  является бернуллиевской
случайной величиной (см. Пример 2.1). является бернуллиевской
случайной величиной (см. Пример 2.1).
Замечание 2.6
См. также Пример 2.4 и Упражнение 2.3.
Предложение 2.3 (Без доказательства.)
Пусть дана последовательность
случайных величин
 такая, что все математические
ожидания
 существуют и
Тогда
- a)
-
 абсолютно сходится абсолютно сходится  , ,
- б)
- существует математическое ожидание
 , ,
- в)
-

Лемма 2.2
Пусть
 --
последовательность несовместных событий:
 . Рассмотрим
случайную величину вида
 |
(8) |
Предположим, что
 Тогда
Доказательство.
Данное утверждение есть следствие сформулированного выше Предложения.
Действительно, обозначим
 . Заметим, что . Заметим, что
 .
Легко проверить, что условия Предложения 2.3 выполнены. Следовательно, .
Легко проверить, что условия Предложения 2.3 выполнены. Следовательно,

Замечание 2.7
Обратим внимание на то, что в бесконечной сумме (8) при любом
фиксированном  только одно слагаемое отлично от нуля. Это вытекает
из несовместности событий только одно слагаемое отлично от нуля. Это вытекает
из несовместности событий  . .
| 


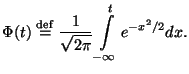

 абсолютно сходится
абсолютно сходится  ,
,
